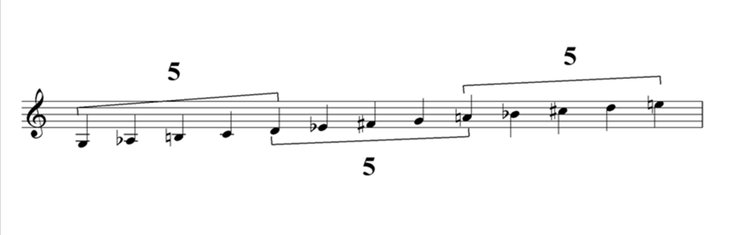
Figure 29: The scale of the 6th Tone in contemporary Eastern Chant, as to be found in contemporary singers’ manuals. (e.g.: Metodi Grigorov, 2005; Petar Dinev, etc.).
____________________________________________
This however is not explained today with the principle of fifth-repeating modes (Chapter 4.1), as reconstructed uniquely in Mechkova’s research. Instead an octave-based description is given, in which ‘certain degrees are altered differently in the different octaves’. Although Mechkova’s description, which is based on an extensive research of primary sources, makes much more sense, I have been curious about the perceptual and cognitive basis for such modes, as octave similarity and respectively octave cyclicity in scalar constructions is claimed by the majority of music psychologists as ubiquitous.149 (click) 150 (click) Sethares posits, however, that there are world cultures that use scales/modes that are not octave-repeating in their scalar structure and furthermore he establishes a connection between that fact and the nature of the spectrum of the instruments these cultures use.151 (click) In his opinion the scalar structures used by a culture is a function of the spectral structure of the timbres of the instruments in use in that culture.152 (click) That is because scales and tunings are constructed in such a way that the optimum perceptual consonance is sought, which itself is determined by the partials of the timbre of the instruments.153 (click) Therefore the optimum scales for the Western classical tradition are determined by the harmonic spectrum of the human voice and the instruments used in our tradition.154 (click) (See also Chapter 2.1.) It is true that in Eastern Chant the only timbre used is the human voice and it has a harmonic spectrum. Therefore the octave cyclicity of modes should be just as ubiquitous as it is in the Western tradition. However, research by Födermayr and Deutsch on the psychoacoustic significance of the Ison in Bulgarian Chant155 (click) has shown that the particular strength of the sixth partial, the physical absence of the fundamental and a particular kind of masking in the process of movement of the chant melody contour, create a very strong psychoacoustic ‘framing’ through the interval of perfect fifth. In their opinion this shapes and ‘anchors’ the harmonic content of the chant156(click) which in my view determines the structure and cyclicity of the mode in this case. Because I would add that in the living practice of singing the chants at church, when the chant develops above the fifth degree of the mode, the Ison will be repositioned to that fifth degree, as it will then become the first degree of the next cycle of the fifth-repeating mode. Thus the new Ison would frame with its overtones the next fifth up, forming the next – upper cycle of the fifth-repeating mode. That might be one of the perceptual reasons for the existence of these fifth-repeating modes in Eastern Chant, from a psychoacoustic/psychological/perceptual/cognitive perspective.
Another reason might be the fact, that with the establishment of modal centre through linear means (Chapter 4.2), any kind of disposition of centres, and respectively – cyclicity of modes could be established within this monophonic context (Chapter 4.2). This could account also for the fourth-repeating modes in Eastern Chant (triphonia), and the diphonia etc.. 157 (click)
Nevertheless, these modes are attributes of the monophonic nature of this tradition, and I have puzzled for a long time whether these could be applied to a non-monophonic, multi-voiced (polyphonic, heterophonic etc.) context in my music, having in mind also that the harmonic timbre of the instruments of the Symphony Orchestra makes the octave very important perceptually, and I use octave doublings extensively, which both have implications for the possibilities for cyclicity of modes employed.
I have attempted to use fifth-repeating modes for the first time in the last movement of the 3rd Percussion Concerto, bars 359-383 (Example 15), which is an extended passage. It is quite an important passage, as it is positioned by the very end of the concerto. The background morphomodal network for that passage of 24 bars could be summarized to its briefest as follows:
____________________________________________